Introduction to Finite State Automata

A finite state automaton is a graph with nodes and edges that can process input. The input is either accepted or rejected. The input is accepted if, when you are finished reading all input, you are at a final state in the automaton. You move between states (or nodes) in the automaton by consuming input. Some edges consume ε (epsilon), the empty string. A final state is usually indicated by the node having a double wall. That’s it.

The figures in this post are made with OpenFST, an open source tool built by Google and NYU to manipulate finite state transducers (the older sibling of finite state automata).

Finite state automata can be used to process regular expressions, do natural language processing, speech recognition, and more. How? Let’s start with regular expressions. NLP and speech, that’s another post.

Regular Expressions

This is not meant to be a guide to regular expressions. There are plenty of those elsewhere. I will assume you’re familiar with the syntax and meaning. For example, a*b+c? matches bc, but not abbcc. To represent this expression with a finite state automaton, we’ll use Thomson’s construction algorithm. Take a minute to read through that page. So, we end up with the following slightly reduced automaton:

ascii.syms: link

Note: ε is the code for ε, the empty string.

$ fstcompile --acceptor --isymbols=ascii.syms regex.fst.txt > regex.fst
$ fstdraw --acceptor --isymbols=ascii.syms regex.fst | dot -Tpng > regex.png

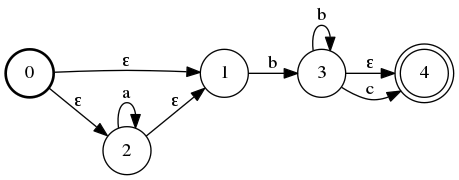
Let’s try processing abbcc with this automaton. You start at state 0 (the one with no input edges). We can’t move to state 1, since we won’t be able to process our first character a. So, we move to state 2 on an ε. We stay at 2 and process the a. We have two bs next. So, we move to state 1 on an ε, move to 3 on a b, then do a loop on 3 with the second b. Finally, we move to state 4 on the first c. Then, we’re stuck – we have input left on the stack, but no way to process it. So, the input string does not match the regular expression.

It’s somewhat difficult to follow the edges around this graph since we sometimes have more than one option of where to move right now. The main cause of this is Thomson’s construction leads to a lot of ε… We can do better.

Properties of Finite State Automata

Two important properties of an automaton are if it is deterministic or minimal. Deterministic means that at every state there is exactly one valid move for each possible input letter. The first automaton was not deterministic since we could move on an ε from state 0 to state 1 or 2. Minimal means exactly what it sounds like – it is impossible to create another automaton which accepts the same language (matches the same regular expression) as this one with fewer states or transitions. Clearly the first automaton was not minimal.

The deterministic and minimal version of the above automaton is:

$ fstrmepsilon regex.fst | fstminimize | fstdeterminize > regex.min.fst
$ fstdraw --acceptor --isymbols=ascii.syms regex.min.fst | dot -Tpng > regex.min.png

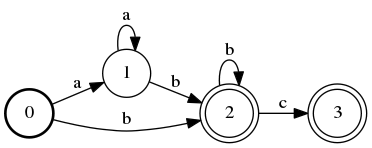
Here, we exploit the fact that we can have more than one final state in our automaton. It’s deterministic because there is exactly one option of where to go from each state – you can’t make any decisions. It’s minimal because you can’t make it any smaller (hand wave).

Finite state automata can also be weighted. Meaning, we can apply a weight to each edge of an automaton. In order to make algorithms play nice, these weights must be on what’s called a semiring. A semiring is essentially a way to make sure certain operations (like determinization) behave properly – it comes bundled with a type of numbers it operates on, a + operator, a x operator, and identity elements for the two operations.

For now, just know when you’re trying to find the best way "through" an automaton for the given input, you want to take the path with the lowest weight. Sometimes, the weights along the path are added together, sometimes they’re multiplied, sometimes it’s something entirely different (you use the + operator for the given semiring). A weighted version of the above automaton might look like this:

regex.w.fst.txt:

$ fstcompile --acceptor --isymbols=ascii.syms regex.w.fst.txt | fstrmepsilon | fstminimize | fstdeterminize > regex.w.fst
$ fstdraw --acceptor --isymbols=ascii.syms regex.w.fst | dot -Tpng > regex.w.png

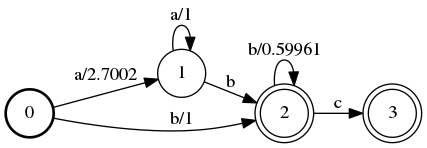
Weighted automata can be used to decide be two alternatives. For example, you’re running a speech recognition system and the user says “I have to go.” How do you know the user didn’t say, “I have two go”? First, you come up with a probability of words occurring next to each other (for example, P("to go") and P("two go")) – a language model. Then, you translate those probabilities into weights for your finite state machine. Then, when you’re deciding between “to” and “two” you pick the sentence with lower weight (“to”).

At first, finite state automata seem to be simple things with a very limited use case. But, they’re useful in a wide range of problems. For example, instead of taking input on the character level, you could input words. Then, your automaton could learn to be a binary classifier of – yes or no – the input is a valid sentence. Finite State Transducers (which can output as well as input) are even more powerful.