Levenshtein Edit Distance With FSTs
Levenshtein edit distance is a metric to tell the difference between two strings. To measure the distance, you count the number of insertions, deletions, and substitutions required to “edit” one string into the other. For example, the edit distance of “two” and “too” is 1 – substitute “w” with “o.” The most common implementation of computing the edit distance of two strings uses dynamic programming (see the Wikipedia page). We’re going to take a different route in this post – finite state transducers.
Here’s the plan: Come up with some transducer that can make the edits, give all of the edits weight 1, then figure out how to apply it to two strings.
Edit Transducer
Our edit transducer needs to support three operations: insert, delete, and substitute. If you can, try to come up with this transducer on your own. If not… To insert a character with a transducer, we can input an ε (the empty string, “") and output the character. To delete, we input some character and output ε. To substitute, we input one character and output another. We also need the “base case,” where we input and output the same character. Easy!
Let’s see what it looks like for the alphabet {a, b, c}. Let’s use a Python script to create the FST, since it can get pretty tedious to make by hand:
Here is a helper bash function to draw an FST:
Now we can put it all together:
$ python make_T.py | fstcompile --isymbols=ascii.syms --osymbols=ascii.syms > T.fst
$ draw T
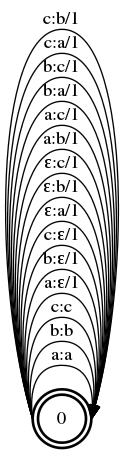
From the top to the bottom of the image, we replace characters (e.g. c:b/1), insert characters (e.g. ε:c/1), delete characters (e.g. c:ε/1), and leave characters unedited (e.g. c:c). So, how do we actually use this? Let’s start with the input. Here’s what happens when you take abc and compose it with the above:
$ fstcompile --isymbols=ascii.syms --osymbols=ascii.syms abc.fst.txt > abc.fst
$ fstcompose abc.fst T.fst > T_abc.fst
$ draw T_abc
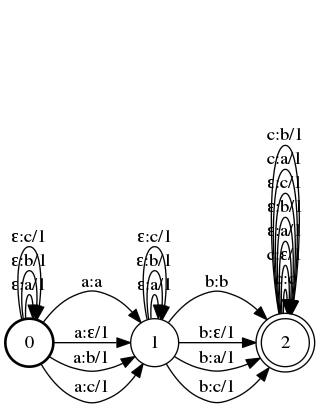
Whoah. That’s a douzy. We can interpret this FST as outputting all possible strings we can edit abc into. Starting at state 0, we can insert a, b, or c (by moving along an edge like ε:a). When we move from state 0 to 1, we can leave the a alone (a:a), delete it (a:ε), or replace it with b or c (e.g. a:b). Same goes for states 1 and 2 with b and c, respectively. The cost of an edit is the sum of all of the weights of your path through the FST (other FSTs might use a different operation than sum).
Using the Edit Transducer
When we’re trying to edit one string into another (to compute the edit distance), we don’t want to score all possible edits of the first string – we only want the ones that are equal to the second string. So, how can we restrict the T_abc.fst output to only show the edits which end up outputting our second string? Another composition!
$ fstcompile --isymbols=ascii.syms --osymbols=ascii.syms cba.fst.txt > cba.fst
$ fstcompose abc.fst T.fst | fstcompose - cba.fst > abc_T_cba.fst
$ draw abc_T_cba
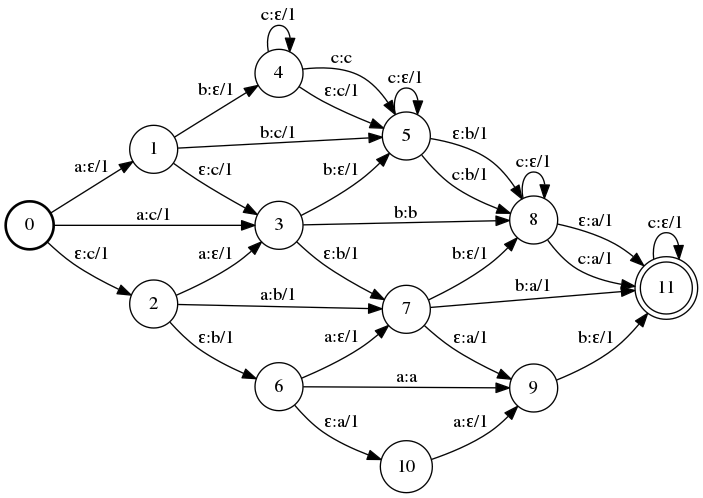
This transducer gives us a lattice of all of the edits we can make which can turn abc into cba. No matter what path you take from state 0 to state 11, you will end up with the string cba. For example, if you trace the path 0 → 1 → 4 → 4 → 5 → 8 → 11, you delete a, delete b, delete c, insert c, insert b, and insert a (for a total cost of 6). The shortest (lowest cost) path is 0 → 3 → 8 → 11 (replace c with a, don’t edit b, and replace a with c for a total cost of 2). Here’s how to calculate the distance with OpenFST:
$ fstshortestpath abc_T_cba.fst > shortest.fst
$ draw shortest

Now, we can compute the Levenshtein edit distance between any two strings in our alphabet! For example:
$ fstcompose cbacbabcaab.fst T.fst | fstcompose - abcbcbcac.fst | fstshortestpath > shortest2.fst
$ draw shortest2
